Continuous Quantum Nondemolition Measurement of the Transverse Component of a Qubit

Abstract

We report the experimental nondemolition measurement of coherence, predictability and concurrence on a system of two qubits. The quantum circuits proposed by De Melo et al. (Phys Rev Lett 98(25):250501, 2007) are implemented on IBM Q (superconducting circuit) and IonQ (trapped ion) quantum computers. Three criteria are used to compare the performance of the different machines on this task: measurement accuracy, nondemolition of the observable, and quantum state preparation. We find that the IonQ quantum computer provides constant state fidelity through the nondemolition process, outperforming IBM Q systems on which the fidelity consequently drops after the measurement. Our study compares the current performance of these two technologies at different stages of the nondemolition measurement of bipartite complementarity.

Access options

Buy single article

Instant access to the full article PDF.

39,95 €

Price includes VAT (Indonesia)

Data availability statement

The code that supports this study is openly available in GitHub at https://github.com/NicoSchwaller/QND-measurement-of-complementarity.

Notes

3. Experiments on 5-qubit backends performed on 23.11.2020 (ibmq_rome V1.2.1), 17.11.2020 (ibmq_vigo V1.3.0), 13.11.2020 (ibmq_5_yorktown V2.2.1). The 15-qubit backend ibmq_16_melbourne V2.3.2 was used on 20.11.2020, and IonQ on weekends from 5.12.2020 to 10.01.2021.

4. The circuit was transpiled with the "optimization_level\(=3\)" argument passed to the Qiskit transpile function, which is the highest available level of optimization.

5. "optimization_level\(=3\)" was enabled except for Fig. 7 and \(\mathscr {C}_2, \mathscr {V}_\mathrm{A}\) in Fig. 8, where the results were better without optimization.

References

1. De Melo, F., Walborn, S.P., Bergou, J.A., Davidovich, L.: Quantum nondemolition circuit for testing bipartite complementarity. Phys. Rev. Lett. 98(25), 250501 (2007). https://doi.org/10.1103/PhysRevLett.98.250501

   Article  Google Scholar

2. Braginsky, V.B., Vorontsov, Y.I., Thorne, K.S.: Quantum nondemolition measurements. Science 209(4456), 547–557 (1980). https://doi.org/10.1126/science.209.4456.547

   ADS  Article  Google Scholar

3. Poizat, J.-Ph., Roch, J.-F., Grangier, P.: Characterization of quantum non-demolition measurements in optics. Ann. Phys. Fr. 19(3), 265–297 (1994). https://doi.org/10.1051/anphys:01994001903026500

   ADS  Article  Google Scholar

4. Ralph, T.C., Bartlett, S.D., O'Brien, J.L., Pryde, G.J., Wiseman, H.M.: Quantum nondemolition measurements for quantum information. Phys. Rev. A 73(1), 012113 (2006). https://doi.org/10.1103/PhysRevA.73.012113

5. Yoneda, J., Takeda, K., Noiri, A., Nakajima, T., Li, S., Kamioka, J., Kodera, T., Tarucha, S.: Quantum non-demolition readout of an electron spin in silicon. Nat. Commun. 11, 1144 (2020). https://doi.org/10.1038/s41467-020-14818-8

   ADS  Article  Google Scholar

6. Shomroni, I., Qiu, L., Malz, D., Nunnenkamp, A., Kippenberg, T.J.: Optical backaction-evading measurement of a mechanical oscillator. Nat. Commun. 10, 2086 (2019). https://doi.org/10.1038/s41467-019-10024-3

   ADS  Article  Google Scholar

7. Hertzberg, J.B., Rocheleau, T., Ndukum, T., Savva, M., Clerk, A.A., Schwab, K.C.: Back-action-evading measurements of nanomechanical motion. Nat. Phys. 6, 213–217 (2010). https://doi.org/10.1038/nphys1479

   Article  Google Scholar

8. Jakob, M., Bergou, J.A.: Quantitative complementarity relations in bipartite systems: entanglement as a physical reality. Opt. Commun. 283(5), 827–830 (2010). https://doi.org/10.1016/j.optcom.2009.10.044

   ADS  Article  Google Scholar

9. Schwaller, N., Dupertuis, M.-A., Javerzac-Galy, C.: Evidence of the entanglement constraint on wave-particle duality using the IBM Q quantum computer. Phys. Rev. A 103(2), 022409 (2021). https://doi.org/10.1103/PhysRevA.103.022409

   ADS  Article  Google Scholar

10. Wootters, W.K.: Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80(10), 2245 (1998). https://doi.org/10.1103/PhysRevLett.80.2245

    ADS  Article  MATH  Google Scholar

11. Cruz, P.M.Q., Fernández-Rossier, J.: Testing complementarity on a transmon quantum processor. Phys. Rev. A 104(3), 032223 (2021). https://doi.org/10.1103/PhysRevA.104.032223

    ADS  Article  Google Scholar

12. Kuzmak, A.R., Tkachuk, V.M.: Measuring entanglement of a rank-2 mixed state prepared on a quantum computer. Eur. Phys. J. Plus 136, 564 (2021). https://doi.org/10.1140/epjp/s13360-021-01553-2

    Article  Google Scholar

13. McKague, M.: On the power quantum computation over real Hilbert spaces. Int. J. Quantum Inf. 11(1), 1350001 (2013). https://doi.org/10.1142/S0219749913500019

    MathSciNet  Article  MATH  Google Scholar

14. Kim, Y.-H., Kulik, S.P., Shih, Y.: Bell-state preparation using pulsed nondegenerate two-photon entanglement. Phys. Rev. A 63(6), 060301 (2001). https://doi.org/10.1103/PhysRevA.63.060301

    ADS  Article  Google Scholar

15. Sisodia, M.: Comparison the performance of five-qubit IBM quantum computers in terms of bell states preparation. Quantum Inf. Process. 19, 215 (2020). https://doi.org/10.1007/s11128-020-02712-7

    ADS  MathSciNet  Article  Google Scholar

16. Fowler, A.G., Mariantoni, M., Martinis, J.M., Cleland, A.N.: Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86(3), 032324 (2012). https://doi.org/10.1103/PhysRevA.86.032324

    ADS  Article  Google Scholar

17. Ristè, D., Poletto, S., Huang, M.Z., Bruno, A., Vesterinen, V., Saira, O.P., Dicarlo, L.: Detecting bit-flip errors in a logical qubit using stabilizer measurements. Nat. Commun. 6, 6983 (2015). https://doi.org/10.1038/ncomms7983

    ADS  Article  Google Scholar

18. Aleksandrowicz, G., et al.: Qiskit: An open-source framework for quantum computing (2019). https://qiskit.org

19. Wright, K., et al.: Benchmarking an 11-qubit quantum computer. Nat. Commun. 10, 5464 (2019). https://doi.org/10.1038/s41467-019-13534-2

    ADS  Article  Google Scholar

20. Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K.: Quantum entanglement. Rev. Mod. Phys. 81(2), 865 (2009). https://doi.org/10.1103/RevModPhys.81.865

    ADS  MathSciNet  Article  MATH  Google Scholar

21. Wootters, W.K.: Entanglement of formation and concurrence. Quantum Inf. Comput. 1, 27–44 (2001). https://doi.org/10.26421/QIC1.1-3

    MathSciNet  Article  MATH  Google Scholar

22. Uhlmann, A.: The "transition probability" in the state space of a \(\ast \)-algebra. Rep. Math. Phys 9(2), 273–279 (1976). https://doi.org/10.1016/0034-4877(76)90060-4

23. Jozsa, R.: Fidelity for mixed quantum states. J. Mod. Opt. 41(12), 2315–2323 (1994). https://doi.org/10.1080/09500349414552171

    ADS  MathSciNet  Article  MATH  Google Scholar

24. Bengtsson, I., Zyczkowski, K.: Geometry of Quantum States: An Introduction to Quantum Entanglement. Cambridge University Press, Cambridge (2006). https://doi.org/10.1017/CBO9780511535048

    Book  MATH  Google Scholar

25. Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2010). https://doi.org/10.1017/CBO9780511976667

    Book  MATH  Google Scholar

26. Wu, Z., Zhu, C., Zhang, X.: Some new metrics based on partial fidelity and partial super-fidelity. Commun. Theor. Phys. 61(1), 37–39 (2014). https://doi.org/10.1088/0253-6102/61/1/06

    ADS  Article  MATH  Google Scholar

27. Linke, N.M., Maslov, D., Roetteler, M., Debnath, S., Figgatt, C., Landsman, K.A., Wright, K., Monroe, C.: Experimental comparison of two quantum computing architectures. Proc. Natl. Acad. Sci. U.S.A. 114(13), 3305–3310 (2017). https://doi.org/10.1073/pnas.1618020114

    Article  Google Scholar

28. Mehdi, Z., Ratcliffe, A.K., Hope, J.J.: Fast entangling gates in long ion chains. Phys. Rev. Res. 3(1), 013026 (2021). https://doi.org/10.1103/PhysRevResearch.3.013026

    Article  Google Scholar

29. Maksymov, A., Niroula, P., Nam, Y.: Optimal calibration of gates in trapped-ion quantum computers. Quantum Sci. Technol. 6(3), 034009 (2021). https://doi.org/10.1088/2058-9565/abf718

    ADS  Article  Google Scholar

30. Amico, M., Dittel, C.: Simulation of wave-particle duality in multipath interferometers on a quantum computer. Phys. Rev. A 102(3), 032605 (2020). https://doi.org/10.1103/PhysRevA.102.032605

    ADS  Article  Google Scholar

31. Mooney, G.J., Hill, C.D., Hollenberg, L.C.L.: Entanglement in a 20-qubit superconducting quantum computer. Sci. Rep. 9, 13465 (2019). https://doi.org/10.1038/s41598-019-49805-7

    ADS  Article  Google Scholar

32. Mandviwalla, F.: Ionq's leading systems now available through qiskit. IonQ Press Release. https://ionq.com/news/april-12-2021-ionq-systems-now-available-through-qiskit. Accessed 21 Aug 2021

33. James, D.F.V., Kwiat, P.G., Munro, W.J., White, A.G.: Measurement of qubits. Phys. Rev. A 64(5), 052312 (2001). https://doi.org/10.1103/PhysRevA.64.052312

    ADS  MathSciNet  Article  Google Scholar

Download references

Acknowledgements

We thank Dr. Marc-André Dupertuis for useful advice, comments and discussions. C.G. acknowledges support from the Swiss National Science Foundation (project nos. 170684 and 198898). This work received funding from the European Union's Horizon 2020 Research and Innovation Program under grant agreement no 820196 (ERC CoG QTONE). We acknowledge use of IBM Quantum and Amazon Web Services' quantum computing service Amazon Braket. We thank very much the Amazon Braket team for their technical help. The views expressed are those of the authors and do not reflect the official policy or position of IBM, the IBM Q team, Amazon or Amazon Web Services.

Author information

Authors and Affiliations

1. Institute of Physics, Swiss Federal Institute of Technology Lausanne (EPFL), Lausanne, CH-1015, Switzerland

   Nicolas Schwaller, Valeria Vento & Christophe Galland

2. Miraex, EPFL Innovation Park, Building L, Lausanne, CH-1015, Switzerland

   Nicolas Schwaller

Corresponding author

Correspondence to Nicolas Schwaller.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Check for (16)

Let \(\rho _{i}\) be the 4-qubit state after state preparation by the circuit of Fig. 1,

$$\begin{aligned} \rho _i=| \chi \rangle \langle \chi |\otimes | 0 \rangle \langle 0 |, \end{aligned}$$

(21)

the two-qubit identity operator \(\mathbb {1}=\begin{pmatrix} 1 &{} 0\\ 0 &{} 1 \end{pmatrix}\), and the rotation along \(\hat{y}\),

$$\begin{aligned} R=\begin{pmatrix} \cos \frac{\pi }{4} &{}\quad -\sin \frac{\pi }{4}\\ \sin \frac{\pi }{4} &{}\quad \cos \frac{\pi }{4} \end{pmatrix}. \end{aligned}$$

(22)

The three-qubit C-NOT gate with first qubit as control and last one as target is written in the usual computational basis as

$$\begin{aligned} \mathrm {CNOT}_{1\rightarrow 3}=\begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ \end{pmatrix}. \end{aligned}$$

(23)

The evolution of \(\rho _i\) through the QND circuit of Fig. 3 is described by the operator

$$\begin{aligned} U_{V}&=(R^{-1}\otimes R^{-1}\otimes \mathbb {1}\otimes \mathbb {1})(\mathbb {1}\otimes \mathrm {CNOT}_{1\rightarrow 3})\\&\qquad (\mathrm {CNOT}_{1\rightarrow 3}\otimes \mathbb {1})(R\otimes R\otimes \mathbb {1}\otimes \mathbb {1}). \end{aligned}$$

It is easy to check that \(U_{V}\rho _iU_{V}^\dagger \) is the state (16).

Quantum state tomography

Quantum state tomography is a procedure by which one can infer the density matrix and requires a complete set of measurements (as many as the number of real parameters in the density matrix). The density matrix holds all the information needed to compute the expectation values of any system observable. In particular, concurrence, coherence and predictability in a two qubit system can be computed from its density matrix, directly using Eqs. (6–8).

On IBM Q machines, a built-in method for quantum state tomography is used: the function "state_tomography_circuits" sets up the circuits needed for two-qubit state tomography, and "StateTomographyFitter" does compute the density matrix using maximum likelihood methods. This technique allows to increase the speed of tomographic measurements, by reducing the number of required circuits. On the IonQ quantum processor, we implement the linear tomography method presented in [33] which consists in the execution of 16 circuits per tomography step. Those two methods, albeit different, are both valid to measure the density matrix of the system.

Table 1 Root of mean squared error of the tomographic measurements on the input state, with respect to the expected values, \(E(\{\mathscr {O}_i^{\rho _\chi }\})\)

Full size table

Table 1 reports the errors of the tomographic measurements (with respect to the theoretically expected value) performed on the state \(|\chi \rangle \). These tomographic measurements of the input states are used as reference measurements to which one can compare the QND method. The values reported in Table 1 show that the quality of the state preparation is not constant: the tomographic measurement is expected to be slightly more efficient than the QND measurement (see "Appendix C", Table 2), in particular because tomography requires less entangling gates. However, significantly higher errors are sometimes observed for the initial tomographic measurement. Up to some point, this could also be due to noise in the measurement process, but in some cases most probably to poor state preparation.

QND and output state measurements

The figures of this section report the QND and tomographic measurements of visibility and predictability. The data are plotted as in Fig. 5: blue squares for IonQ, red circles for IBM Q, which are filled (QND) and empty (tomography). Crosses are used for the output state, and a black line shows the theoretical expectation computed with the definitions given in Sect. 2.1.

Table 2 Root of mean squared error of the QND measurements on the input state \(E(\{\mathscr {O}_i^\mathrm{QND}\})\)

Full size table

Fig. 11

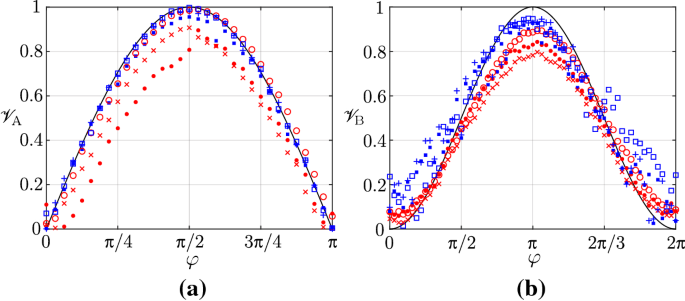
Visibility of input state \(|\chi \rangle \) measured by the QND circuit (filled symbols) and the state tomography (empty symbols), using ibmq_rome (red) and IonQ (blue) quantum bits, and measurements of visibility on the output state \(|\psi \rangle \) (crosses). a \(\mathscr {V}_\mathrm{A}\), \(\theta =0\) (theoretical expectation \(\mathscr {V}_\mathrm{A}(\varphi )=\sin \varphi \)), b \(\mathscr {V}_\mathrm{B}\), \(\theta =\frac{3\pi }{2}\) (theoretical expectation \(\mathscr {V}_\mathrm{B}(\varphi )=\frac{1-\cos \varphi }{2}\)). The symbols follow the convention of Fig. 5 (Color figure online)

Full size image

Fig. 12

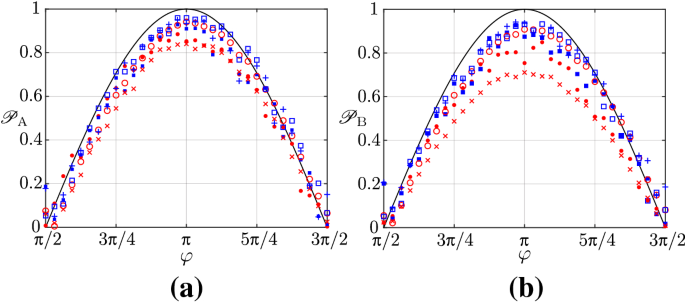
Predictability \(\mathscr {P}_\mathrm{A}\) (a) and \(\mathscr {P}_\mathrm{B}\) (b) of the input state \(|\chi \rangle \) (\(\theta =\pi \)) measured by the QND circuit (filled symbols) and the state tomography (empty symbols), using ibmq_rome (red) and IonQ (blue) quantum bits, and measurements of predictability on the output state \(|\psi \rangle \) (crosses). Theoretical expectations (black lines) are \(\mathscr {P}_\mathrm{A}(\varphi )=\mathscr {P}_\mathrm{B}(\varphi )=-\cos \varphi \). The symbols follow the convention of Fig. 5 (Color figure online)

Full size image

In opposition to concurrence, as piloting \(\mathscr {V}_\mathrm{A}\) requires only the local rotation defined by the angle \(\varphi \), the state preparation is more efficient than for entangled states (Fig. 11a). In fact, one can see that the QND measurement gives an excellent measurement of \(\mathscr {V}_\mathrm{A}\) on IonQ. The measurement on the output state is also very close to the expected value, for the full range of analyzed states. While the state preparation on IBM Q is satisfying (input state tomography, empty red circles in Fig. 11a), a significant gap to the expected result appears for the QND measurement and the output state characterization on ibmq_rome. Varying the visibility of the qubit \(\mathrm{B}\) with the state preparation circuit of Fig. 1 requires a nonzero value of \(\theta \), a more costly operation than when studying \(\mathscr {V}_\mathrm{A}\). The measurements of \(\mathscr {V}_\mathrm{B}\) (Fig. 11b) seem more noisy for IonQ than IBM Q, and it cannot be determined visually which machine gives the most accurate result. However, looking at the peak value of \(\mathscr {V}_\mathrm{B}\) at \(\varphi =\frac{\pi }{32}\), IonQ seems to perform better. Coming to predictability, we measure \(\mathscr {P}_\mathrm{A}\) and \(\mathscr {P}_\mathrm{B}\) on the same quantum states (i.e., the same values of \(\varphi ,\theta \)). This enables to compare values (\(\mathscr {P}_\mathrm{A}\) and \(\mathscr {P}_\mathrm{B}\)) truly measured at the same time on the same quantum system. On IBM Q (red data in Fig. 12), an asymmetric behavior is observed: the measured predictability of the qubit \(\mathrm{B}\) is more distant from the expected value than the one of qubit \(\mathrm{A}\). One can clearly see a higher deviation in the QND and final tomography measurements of \(\mathscr {P}_\mathrm{B}\) on IBM Q for qubit \(\mathrm{B}\). This is the case around \(\varphi =\pi \), where \(|\chi \rangle =|11\rangle \). The excited state of the second qubit (\(\mathrm{B}\)) is prepared through the C-NOT gate, a process which may be responsible for the degradation of the state of qubit \(\mathrm{B}\) with respect to qubit \(\mathrm{A}\). The mean error between the measurements and the theoretically expected values is reported for each machine and for each observable in Table 2 (QND measurements) and Table 3 (output state tomographic measurements). In Table 4 and Fig. 13 we show the error between the value of the observable measured via QND and the one obtained by the following destructive tomography. We expect the decoherence happening between the two measurements to increase the error from the QND to the tomography, i.e., positive values in Table 4 and Fig. 13. Negative values appear when the measurement noise is high compared to the degradation of the state between the two measurement steps. Note that \(\mathscr {C}_2\) (followed by \(\mathscr {C}_1\)) is the measurement for which the state is most likely to experience decoherence, and in that case we observe an actual degradation from the QND to the tomographic measurement for every machine: Fig. 13. One can see that using IonQ, the two measurements are relatively close (black dashed line in Fig. 13). Indeed, as shown in Fig. 6, the quantum state is robust to decoherence between the two measurements on IonQ. On IBM Q, we observed considerably higher degradation of the state between the two steps, but also some unexpectedly high measurement errors. The backend ibmq_rome seems not to be subject to these errors, thus we can observe the effective degradation of the state between the measurements (blue dashed line in Fig. 13). Finally, we may remark that the optimization of the quantum circuits on IBM Q does not result in any notable improvement in most cases.

Table 3 Root of mean squared error of the tomographic measurement on the output state \(E(\{\mathscr {O}_i^{\rho _\psi }\})\)

Full size table

Table 4 Mean error between the QND measurement and the subsequent tomographic estimation, \(E(\{\mathscr {O}_i^{\rho _\psi }\})-E(\{\mathscr {O}_i^\mathrm{QND}\})\)

Full size table

Fig. 13

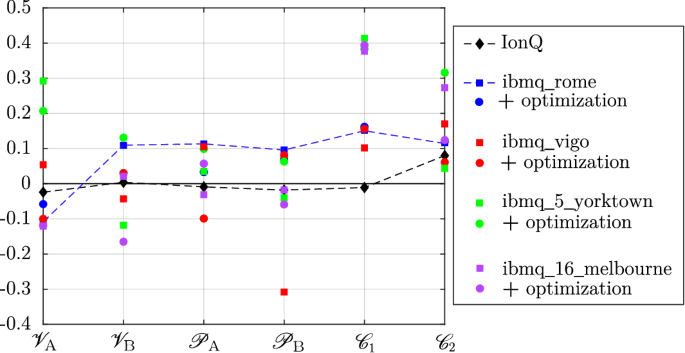
Mean error between the QND measurement and the subsequent tomographic estimation, \(E(\{\mathscr {O}_i^{\rho _\psi }\})-E(\{\mathscr {O}_i^\mathrm{QND}\})\). Dashed lines are traced between results of IonQ (black), which most of the time provide the smallest error, and ibmq_rome (blue), the best performing IBM Q backend (Color figure online)

Full size image

Quantum state preparation criterion

Figure 14 shows the probability amplitudes of the quantum states of Eqs. (16–18). The states with sufficiently high probability amplitude (see Figs. 7 and 8) are postselected before measurement of the observables, i.e., using the QND measurement as a state preparation circuit. The average value measured on those states is reported in Table 5 for each observable.

Fig. 14

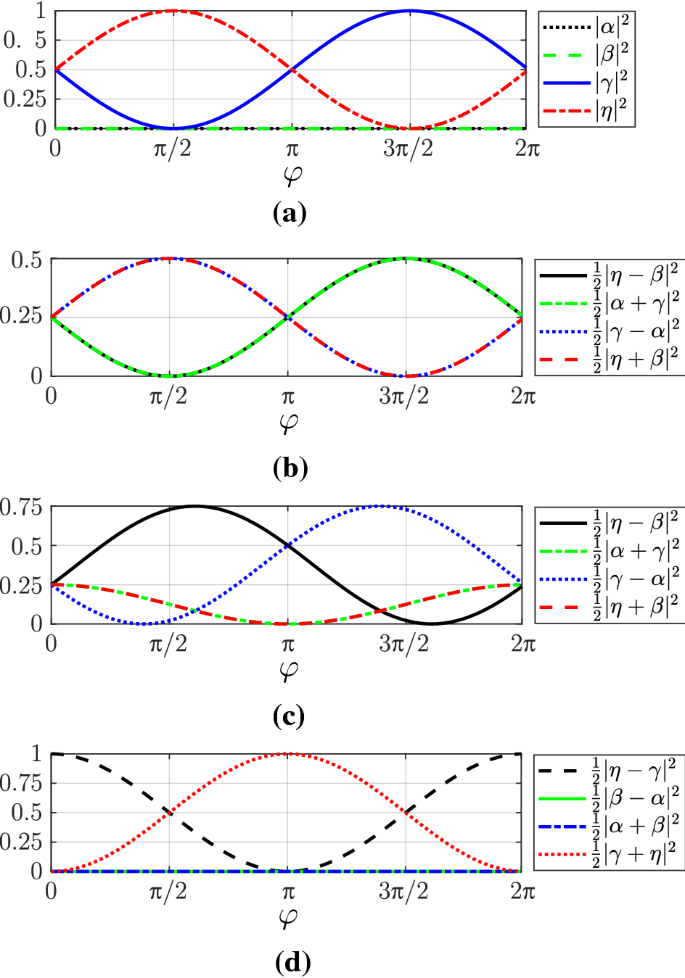
Probability amplitudes of the output states of Eqs. (16–18) for the measurement settings of a \(\mathscr {C}\) with \(\theta =\pi \) b \(\mathscr {V}_k\) with \(\theta =0\) c \(\mathscr {V}_k\) with \(\theta =3\pi /2\) and d \(\mathscr {P}_k\) with \(\theta =\pi \)

Full size image

Fidelity measurements

We computed the mean fidelity (20) of all relevant states \(|\chi \rangle \) (\(|\psi \rangle \)) for each observable and reported it in Tables 6 and 7. The fidelity of the postselected states is given in Table 8. Fidelity tends to decrease with the postselection (see Fig. 9 which summarizes Tables 6, 7 and 8). To illustrate this fact, Fig. 15 reports the repetition of the experiment for the measurement of maximal \(\mathscr {V}_\mathrm{B}\) state (\(\theta =\frac{3\pi }{2},\varphi =\pi \)). As observed in general, the mean fidelity is slightly decreased by postselection on ibmq_rome, and close to unchanged on IonQ. In the end, it is clear that postselection does perform efficient state preparation, even healing the measured value of an observable in the case of an incoming eigenstate.

Table 5 Mean value of the measured observable on the conditional states \(|(\psi |_{\omega })\rangle \), postselected as in Figs. 7 and 8

Full size table

Table 6 Mean fidelity of the states \(|\chi \rangle \) generated for the measurement of each observable

Full size table

Table 7 Mean fidelity of the states \(|\psi \rangle \) after the QND measurement

Full size table

Table 8 Mean fidelity of the conditional states \(|(\psi |_{\omega })\rangle \) postselected as in Figs. 7 and 8 after the measurement of each observable

Full size table

Fig. 15

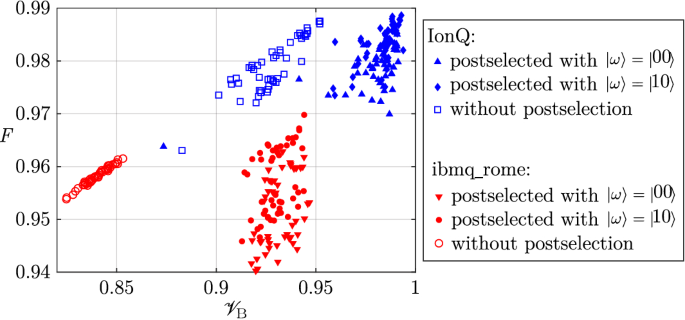
Fidelity as a function of \(\mathscr {V}_\mathrm{B}\) measured on the output state, using the circuit of Fig. 3. 50 repetitions using the \(\mathscr {V}_\mathrm{B}=1\) input state (i.e., \(\theta =\frac{3\pi }{2},\varphi =\pi \))

Full size image

Fig. 16

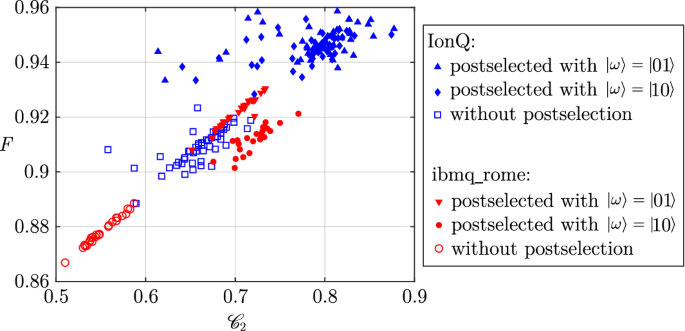
Fidelity as a function of concurrence measured on the output state, using the circuit of Fig. 3. 50 repetitions using the input state \(|\chi \rangle =|\varPhi ^+\rangle \)

Full size image

Indeed, in the case of the measurement of concurrence with the circuit of Fig. 5 (\(\mathscr {C}_1\)), IonQ provides sufficient state fidelity so that postselection does not result in higher concurrence, in opposition to ibmq_rome, on which postselection clearly purifies entanglement (Fig. 10). In the case of \(\mathscr {C}_2\), for which the state is even more fragile and affected by decoherence, postselection happens to be useful to this end on both systems (Fig. 16), clearly increasing the state fidelity together with the target value of the observable. We observed that the difference in the tomography procedure used on IBM Q and IonQ (see "Appendix B") is the main contribution to the higher noise (thicker spreading of the measurements along the line) for IonQ in the results of Figs. 10, 15 and 16. In fact, in opposition with IBM Q, the method we used on IonQ produces matrices that are not necessarily positive semi-definite. They are nevertheless valid estimations of the density matrix of the considered two-qubit state, and the aforementioned artifact does not hinder comparisons of the mean value of observables and fidelity done in this study.

Rights and permissions

About this article

Cite this article

Schwaller, N., Vento, V. & Galland, C. Experimental QND measurements of complementarity on two-qubit states with IonQ and IBM Q quantum computers. Quantum Inf Process 21, 75 (2022). https://doi.org/10.1007/s11128-021-03354-z

Download citation

• Received: 20 July 2021

• Accepted: 10 November 2021

• Published: 29 January 2022

• DOI : https://doi.org/10.1007/s11128-021-03354-z

Keywords

• Quantum nondemolition (QND)
• Complementarity
• Entanglement
• Qubits
• Trapped ions
• Superconducting
• IonQ
• IBM Q

lip112.blogspot.com

Source: https://link.springer.com/article/10.1007/s11128-021-03354-z

Berbagi :